产品类别
新闻分类导航
联系我们
厂家传真：022-83719059
企业邮箱：hjzhu0518@21cn.com 工厂所在地址： 天津市南开区华苑产业区鑫茂科技园D2座一层A单元
新闻详情
基于函数插值的柯氏质量流量计信号处理方法
0 引言
柯氏质量流量计（CMF— Coriolis mass flowmeter），它是利用流体流过振动管道时产生的柯里奥利（Cociolis）效应，对管道的两端振动的相位的影响来实现流体质量流量的测量[1]。
目前，大多数的柯氏质量流量计相位差的求取，都采用基于离散傅利叶变换（DFT）数字信号处理方式。对于这种方式来说，如何保证信号的整周期采样是影响其精度的关键所在。很多研究的重点都放在了如何确定当前信号的频率这个问题上，而没有有效地解决整周期采样的问题。文献[2]提出频率粗测和细测的方法，并且用这个频率去修改A/D转换器下一次的采样频率，以实现整周期采样；文献[3-4]的方法，采用一段时间内频率变化的平均值作为改变下一次采样频率的依据。不管这些方式对确定当前信号频率的精度有多高，它们的实质是一样的，都是用当前信号的频率，预测地修改下一次的采样频率。我们知道这对频率变化的信号来说，不可能实现信号的整周期采样，尤其是对于频率突变的信号（振动管中有气泡）来说，这样会引起较大的固有测量误差。
本文给出了一种全新的方法，是在双通道同步A/D转换器（两路信号同时进行采样）采样频率固定不变的情况下，不需要改变A/D转换器的采样频率，利用软件的方法实时获得信号的频率，并且根据这个频率通过函数插值方式，对输入信号序列进行整周期采样转换。该方法在实验中给出了极高的频率及相位差的求取精度。
1 函数插值
在科学与工程计算中，常会碰到函数表达式未知的情况，仅知道该表达式的一些采样点处的函数值，而又需要计算非采样点的数据这类问题，此时希望建立该未知函数的一个便于计算的近似表达式。这就称为函数插值问题。插值函数的种类有很多，最简单的是线性插值，即用过相邻两个采样点的直线来代替原函数f（x）。如图1中a，b是两个采样点，坐标分别为（x1，y1），（x2，y2），过a，b的曲线是原函数F（x），线性插值就是用过该两点的直线L（x）来近似表示F（x）。
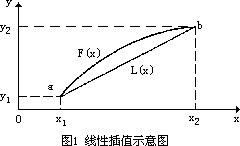
过a，b两点的直线方程可由两点式写出：
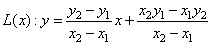其中 x1≤x≤x2 （1）
对于这个方程只要每给出一个x值，就可以求出一个y值。我们可以看出，用直线代替曲线会带来误差，但是只要采样频率足够高，就可以使误差忽略不计。关于其它类型的插值方式可以具体见文献[6]。
2 信号频率的确定
双通道同步A/D转换器每次输出的32位数据，包含该采样时刻两路信号的数字量（各占16位），对于每一路信号来说，如果我们知道了在固定采样频率（Fs）下一个信号周期的采样点数N，那么信号的周期为：N×Ts=N/Fs。我们知道如果采样频率不是信号频率的整数倍的话，那么采样点数N 也不可能包含整个信号周期。
由图2中可以看出，采样点a，b，c，d分别跨在信号过零点e，f的两端，这就使得我们在用上述方法求解信号频率时，会带来较大的误差。
因此，对于任意的输入信号序列，我们作如下的搜索：
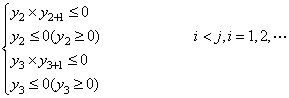（2）
获得符合条件的距离最近的i，j值，即它们表示信号一个周期两端距离过零点最近的点（如图2中a，c点），（括号内表示输入信号反相的情况）。用N 表示：
N=j- i （3）
因此，只要我们能确定出信号一个周期的两个过零点，那么，就可以准确地求解出信号的周期。根据数学知识我们知道，信号Asin（2πft+φ）在过零点附近近似一条直线，因此，可以用几何方法确定出信号的过零点。对于图2的信号，
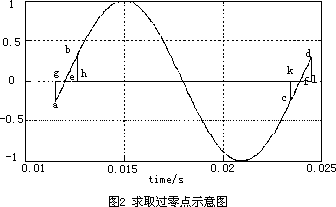
假定a，b点的采样值分别为ya，yb，那么就可以由下式
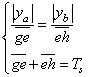（4）
求解出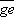 
，它表示过零点e相对采样点a 的延迟时间。同理，可以求出过零点f 相对采样点k的延迟时间 
。
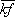那么信号周期就可以表示为：
T=N×Ts+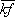 
- 
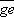（5）
3 采样频率的整周期转换
根据文献[6]对正弦波采样时，每个周期至少采样3个点，采样频率应是信号频率的整数倍数 ，否则会产生较大的频谱泄漏。又因为要采用快速傅里叶算法，则必须保证采样点数是2的整数次幂（本文每周期采样128次）。
本文使用一个较高的固定采样频率（本文用10kHz）对两路信号进行采样，由于不是信号的整数倍采样，所以先要通过函数插值的方法，重新得到信号的整数倍采样数据。
具体的做法是，首先根据式（2）~（5）计算出信号的周期，接着相信号的这个周期128等分，这128个等分点便是整周期采样需要得到数据的采样时刻；然后使用线性插值的方法，得到这些整数倍采样时刻的数据。
假设我们确定出了图2中的信号周期为T，那么整周期采样时的采样周期为：
t's=T/128
为了不引入初始相位，整周期重新采样时刻必须从过零点开始（如图2中e点），以t's为步长。因此：
t's=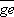
+i×t's，i=0，1，…，127 （6）
其中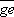
表示如图2中的过零点相对于a点的时间延迟，这由上面已经求出。
我们知道，进行相位差求取时，必须从同一时刻对两路信号分别进行相位求取（如图3中a，c点），因此，在采样频率的整周期转换时，也必须从同一时刻开始对两路信号采样频率进行整周期的转换。为此，采用如下的方法：
对于采样得到的信号序列使用式（2）~（5），先确定出信号的准确周期。
接着，必须从同一时刻开始，分别取出两路信号在这个周期内的采样数据。（如图3中，signal1从点c~d，signal2从点a~b）。
最后，分别对这两组采样数据序列根据式（6）、（1）求出各自的整周期重新采样数据（插值数据）。
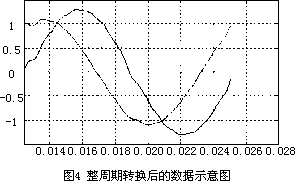
图4是经过上述过程后得到的整周期采样数据（线性插值），图中截取了一个周期。
在实际应用中两路信号的相位差很小，为了能够清楚的在图中画出两路信号的示例，图3，图4中取了较大的相位差；两图中的信噪比SNR=40db。
4 相位差求取
对两路不同频率信号的每个周期都进行128点的快速离散傅里叶变换（DFT），由数学知识我们知道，假定两路信号DFT后，基波分量分别为：x1+y1i，x2+y2i，
则：θ1=arctan（y1/x1），θ2=arctan（y2/x2），
那么，Δθ=θ1- θ2。
5 仿真结果
表1给出了在采样频率Fs=10kHz下，当信号的频率变化时，系统仿真得出的仿真结果。f，Δf分别表示实际给定频率、算出的频率与实际频率的差值（表中单位：赫兹）。
表1 仿真结果 Hz
