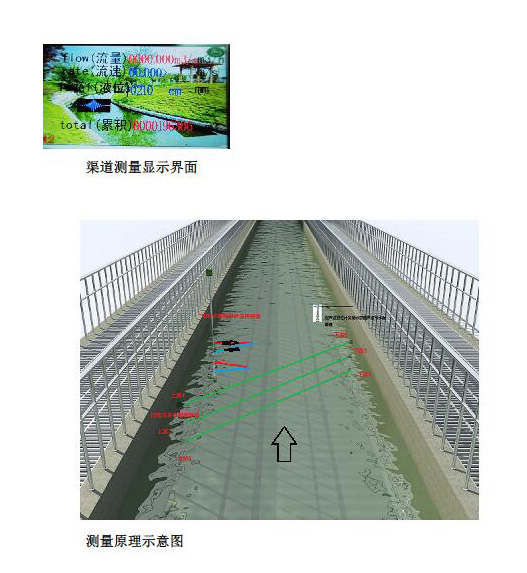
产品类别
新闻分类导航
联系我们
厂家传真:022-83719059
企业邮箱:hjzhu0518@21cn.com 工厂所在地址: 天津市南开区华苑产业区鑫茂科技园D2座一层A单元
新闻详情
基于Fluent的新型微流量热分布式质量流量计的仿真分析及实验研究
一、引言
液体的质量流量是工业测量中极其重要的参数,随着液体系统向微小化方向的发展,对微流量质量流量计的需求也越来越多,但是常用的流量计难以直接应用于微流量测量系统中,测量的自动化程度不高、操作复杂。
针对目前微流量测量中的上述问题,提出了一种新型微流量 T热分布式质量流量计,它没有可动部件、结构简单、维护方便,而且简化了测量过程,降低了成本,适合于液体微小流量的测量。
二、热分布式质量流量计的原理
热分布式质量流量计的工作原理如图1所示,测量管外壁中间绕着一组镍镉加热丝,通过加热器给管道进行加热,测量管外壁对称两端绕着两组长度,阻值大小都相等的铜丝线圈,并与另外两个电阻组成惠斯登电桥。铜丝线圈作为测温元件。由加热器供给镍镉加热丝恒定热量,热量通加热线圈、管壁传导热量给管内流体。

图1 热分布式质量流量计的工作原理
在流体静止时,测量管上的温度分布如图2中虚线所示,相对于测量管中心的上下游是对称的,由铜丝线圈和电阻组成的电桥处于平衡状态;当流体流动时,流体将上游的部分热量带给下游,导致温度分布变化如图2中实线所示,由电桥测出两组线圈电阻值的变化,求得两组线圈平均温度差,便可按下式导出质量流量:
 (1)
(1)
其中,qm—质量流量;
ΔT—平均温度差;
K—仪表常数;
A—测量管绕组(即加热系统)与周围环境热交换系统之间的热传导系数;
Cp—被测气体的定压比热容。

图2 测量管道轴向温度分布
三、改进型热分布式质量流量计
但是,在一些特殊环境比如狭小空间、功率有限、微小流量即低流速(ν<1m/s)、微小管道(壁厚1mm,内径Φ4mm),宽温度范围(0℃~200℃),传统的热分布式质量流量计无法进行测量,所以在这些情况下,对传统热分布式质量流量计结构进行改造,拓展其使用范围,使其可以应用在以上恶劣环境中,如图3所示。

图3 测量管道
在测量管道长度(206mm)有限的情况下,经过理论计算,需要的加热丝无法全部紧密绕在普通测量管道上面,所以经过加工改良,我们把测量管中心加粗,如图3(b)所示,这样加热丝就可以全部绕在管道中间凸起外侧。与管道接触部分要窄于凸起部分外侧,这是希望加热丝的热量就能够更加集中地传递到受热流体部分,以达到更好的加热效果。
根据电热丝的电功率,传热公式可得:
 (2)
(2)
其中:U—加热丝两端的电压,单位:V;
λ—金属管道的导热系数,单位:W/(m•℃);
ΔT—管道内水流升高的温度,单位:℃;
h—测量管道中间凸起部分的高度,单位:m;
R—加热丝的阻值,单位:Ω;
R=αl
S—加热丝绕管道的侧面积,单位:m2;
S=2πL(h+d)
α—加热丝的电阻比,单位:Ω/m;
l—加热丝的长度,单位:m;
d—中心细管的内径,单位:m;
L—加热丝绕管道的宽度,单位:m。
在常见的金属里面,纯铜的导热性能最好,所以我们在做实验的时候就选取纯铜作为测量管道的材料,它在常温下的导热系数为398W/(m•℃),加热丝选取型号为Cr20Ni80的镍镉丝,它在常温下的电阻比为11.32Ω/m。
通过以上公式的计算我们可以得到所需要的镍镉加热丝的长度、测量管道中间凸起部分的高度,以及测量管道凸起部分的宽度。
四、流场仿真
1、几何模型的建立
使用Autocad软件对新型热分布式质量流量计进行几何模型建立,测试管道长206mm,内径φ4mm,外径6mm,壁厚1mm,其他参数如图4所示。

图4 管道参数
2、网格划分
网格划分是整个计算机仿真过程的关键之一,计算求解能否正确,结果能否满足要求,都与网格划分密切相关,利用Fluent自带的前置处理软件Gambit对新型热分布式质量流量计的几何模型进行网格划分。考虑到计算精度和计算时间,对流量计进行结构化网格划分,采用的网格类型为Submap,即将不规则的区域划分成多个规则的子区域,管道中间凸出部分采用较为粗糙的的四面体网格,管壁和流体部分采用较为细致的四面体网格,使其在计算速度、精度和稳定性等方面达到综合最佳,图5所示。

图5 网格划分
3、边界条件设置
在Gambit中对图中的边界条件设置为:左端入口条件设置为速度入口(velocity-inlet),右端出口条件设置为自由出口(outflow),中间凸起部分最外侧设置为热源(wall),流体与管壁的交界面设置为壁面(wall),其余均为默认设置;然后指定图中连续区域的类型为:中间流体部分为fluid,两端管壁部分为solid。
4、Fluent求解设置
使用Fluent2D单精度求解器,将划分好的流量计结构网格文件导入Fluent中进行计算。Fluent中的设置如下,将尺寸单位改成mm,选择能量方程,材料选择水和铜,边界条件中热源温度设置为573K,流体与管壁的交界面设定为coupled,入口速度为0.1m/s,其余均为默认设置。把收敛准则设为0.001,设置迭代次数为1000次,对入口进行初始化,然后进行迭代求解。经过一定的迭代次数以后,结果收敛,求解完成,如图6所示。

图6 迭代求解
5、计算结果
根据迭代计算收敛的结果,所得的管道温度分布图如图7所示,不同的颜色代表不同的温度,中间红色部分为最高温度,中间水流深蓝色部分为最低温度。水流将一部分热量带到管道下游,与管道对称的上游部分形成温差ΔT,通过此ΔT与水的质量流量可以建立一个关系图。

图7 管道温度分布
五、实验结果
本实验按照图8所示装置进行测量。

图8 实验装置图
按照仿真过程对管道不同速度(ν<1m/s)下的温度场进行仿真,可以得出质量流量与温差之间的关系。然后通过实验装置对真实管道的质量流量进行测量,同样得出质量流量与温差之间的关系。综合仿真结果与实验测量结果通过Matlab画出图9中的两条曲线。

图9 质量流量与温差的关系
图9中红色曲线为Fluent仿真出来的数据,可以看出水流静止的时候,冷热两端温差为零,随着水流缓缓流动,温差从0℃很快升到150℃,而当水流速度继续增加的时候,冷热两端的温差反而开始下降,而且下降速度很快,但随着水流速度继续增加以后,温差继续降低,但降低的速度开始减缓,趋于线形递减。图中黑色曲线为实验测试的数据,从图中可以看到,曲线的起始点并不是零,这是因为实验条件所限,无法测得水流从0~0.1m/s的速度。但是实验测得数据与Fluent仿真的数据(开始下降的部分)趋势基本一致。
六、实验结论
本文利用Fluent软件对新型微流量热分布式质量流量计的管道流场进行仿真,通过仿真知道了质量流量与管道冷热端温差之间的变化关系,然后经过实验验证了此关系是正确的。建议通过改进管道结构,使得二者关系趋于简单线形化,易于测量。